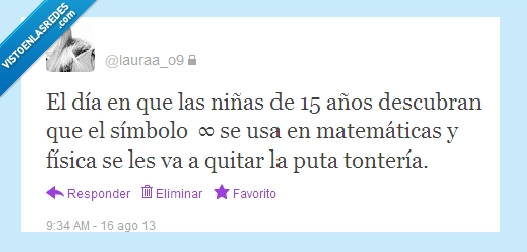
Ya no mola tanto, eh... por @lauraa_o9
Vía: https://twitter.com/lauraa_o9/status/368274627312635905
Nada más rastrero que enviar tus propios tuits, creyéndote la puta pera. Encima el tuit es una puta basura, un ataque gratuito a las niñas de 15 años, que hagan lo que hagan siempre habrá una gilipollas de 18 que les insultará y les dirá cómo vivir la vida con dignidad, como si ellas no hubieran tenido 15 años nunca ni hubieran hecho gilipolleces. Eso sí que me revienta, que tengan que meterse con niñas pequeñas para poder creerse un poco superiores.
15 años son necesarios para saber eso creo que lo sabia desde la primaria
Triste será si con 15 años aun no lo sabe.
No entiendo como ese "descubrimiento" podría quitarle la tontería a alguien ¿Por qué?
ver ese gif y recordar a willie colon
este simbolo se supone que lo debes saber desde primaria, otra cosa es saber lo que representa el simbolo (cero dividido entre cero)
#8 #8 acid_snake dijo: este simbolo se supone que lo debes saber desde primaria, otra cosa es saber lo que representa el simbolo (cero dividido entre cero)¿Cero dividido entre cero? ¿En serio?
#8 #8 acid_snake dijo: este simbolo se supone que lo debes saber desde primaria, otra cosa es saber lo que representa el simbolo (cero dividido entre cero)por favor indagad un poco antes de votarme a negativos, panda de incultos
#9 #9 nib dijo: #8 ¿Cero dividido entre cero? ¿En serio? la definición matematica de la división, tomando como ejemplo la formula x/y = z, es:
buscar un numero z, que al multiplicarlo con y, nos de x.
Aplicandolo a 0/0, tenemos que encontrar un numero que, al multiplicarlo por 0, nos de 0.
Cualquier persona con un mínimo de conocimmiento en metematicas sabe que cualquier número multiplicado por 0 es 0, es decir, el resultado de 0/0 es cualquier número -> infinito.
#10 #10 acid_snake dijo: #8 por favor indagad un poco antes de votarme a negativos, panda de incultos
#9 la definición matematica de la división, tomando como ejemplo la formula x/y = z, es:
buscar un numero z, que al multiplicarlo con y, nos de x.
Aplicandolo a 0/0, tenemos que encontrar un numero que, al multiplicarlo por 0, nos de 0.
Cualquier persona con un mínimo de conocimmiento en metematicas sabe que cualquier número multiplicado por 0 es 0, es decir, el resultado de 0/0 es cualquier número -> infinito."Cualquier número -> infinito". ¿Desde cuándo? Precisamente el hecho de que cualquier número multiplicado por 0 dé 0 hace que 0/0 sea una indeterminación, no infinito, como dices tú.
#11 #11 nib dijo: #10 "Cualquier número -> infinito". ¿Desde cuándo? Precisamente el hecho de que cualquier número multiplicado por 0 dé 0 hace que 0/0 sea una indeterminación, no infinito, como dices tú. 0/0 es una indeterminación por el simple hecho de ser infinito, o acaso "infinito" no significa "cualquier número"? por lo menos en el ámbito matemático, corrigeme todo lo que quieras pero es así como me lo enseñaron en cálculo, estadística y ampliación de las matematicas, ahora a ver si mis profesores de universidad están equivocados :s
#12 #12 acid_snake dijo: #11 0/0 es una indeterminación por el simple hecho de ser infinito, o acaso "infinito" no significa "cualquier número"? por lo menos en el ámbito matemático, corrigeme todo lo que quieras pero es así como me lo enseñaron en cálculo, estadística y ampliación de las matematicas, ahora a ver si mis profesores de universidad están equivocados :sCalcula los limites de f1(x)=x/x, f2(x)=x/x^3 y de f3(x)=x^2/x cuando x tiende a 0 y dime si te dan infinito las tres...
Yo si fuera tu volvería a leer mis apuntes de limites.
#13 #13 assassin90 dijo: #12 Calcula los limites de f1(x)=x/x, f2(x)=x/x^3 y de f3(x)=x^2/x cuando x tiende a 0 y dime si te dan infinito las tres...
Yo si fuera tu volvería a leer mis apuntes de limites.yo que tu volvería a leer mi comentario porque no hablo de límites en ningun sitio, te lo has sacado del culo
#12 #12 acid_snake dijo: #11 0/0 es una indeterminación por el simple hecho de ser infinito, o acaso "infinito" no significa "cualquier número"? por lo menos en el ámbito matemático, corrigeme todo lo que quieras pero es así como me lo enseñaron en cálculo, estadística y ampliación de las matematicas, ahora a ver si mis profesores de universidad están equivocados :sEs que de hecho, la división de cualquier número entre 0 no tiene un resultado definido. En cambio, la de cualquier número por algo que se acerca a 0 sin llegar a ser 0 sí que lo tiene, y es precisamente lo que calculas con los límites.
El límite de 0/x cuando x tiende a 0 (que es lo que más se aproxima a la operación 0/0 sin ser indeterminado) da 0, no infinito.
#14 #14 acid_snake dijo: #13 yo que tu volvería a leer mi comentario porque no hablo de límites en ningun sitio, te lo has sacado del culoBieeeennn... Ahora imaginate porque existen los limites, date cuenta, no se puede dividir por 0 y sacar un resultado de la galera asi porque si, es una indeterminación y a una operación en la cual hay una o el resultado no existe dentro del campo en que se estudia o se usa limites para tratar de resolver la indeterminación, pero ojo, que el limite tenga un resultado numérico (osea que exista el limite) eso no implica que exista le resultado de la operación, por ejemplo si haces f(x)=x/x y resuelves f(0)="Eso No Existe!!", pero el limite cuando tiende a 0 si existe y es un numero (1).
#16 #16 assassin90 dijo: #14 Bieeeennn... Ahora imaginate porque existen los limites, date cuenta, no se puede dividir por 0 y sacar un resultado de la galera asi porque si, es una indeterminación y a una operación en la cual hay una o el resultado no existe dentro del campo en que se estudia o se usa limites para tratar de resolver la indeterminación, pero ojo, que el limite tenga un resultado numérico (osea que exista el limite) eso no implica que exista le resultado de la operación, por ejemplo si haces f(x)=x/x y resuelves f(0)="Eso No Existe!!", pero el limite cuando tiende a 0 si existe y es un numero (1).Nada, nada, que él tiene que llevar la razón por cojones.
Un poco de humor!! Y menos pique!! estamos para divertirnos, o eso creo... :O
A lo que se refiere el colega es que las niñas adolescentes de hoy en dia, cuando se echan un novio se "piensan" que les durara para siempre... y respecto a q: se les quitara la tonteria, me imagino que no lo querran poner mas pq hoy en dia les cuesta muchisimo mates y fisica... es algo q "odian"...
Y la verdad, al menos en mi opinion, hay niñas de 12 años q se emocionan muchisimo con estas cosas... creo q todos lo vemos, shorts que parecen bragas, tops... En mi generacion los padres eran mas autoritarios y controlaban mas... Y mira q tengo 23 años, tmp hay tanta diferencia entre una y otra generacion..
Deja tu comentario
Necesitas tener una cuenta en VistoenlasRedes.com para poder dejar comentarios.¡Registra tu cuenta ahora!








17 ago 2013, 17:19
Con 12 años ya sabes que se usa en matematicas si no tienes un cromosoma de mas....