Profe, no te rayes por @Mejoresexamenes
Vía: https://twitter.com/MejoresExamenes/status/427413710794002432
Si no sabe solucionar eso... su vida no tiene solución, es tonto y ya.
Ya podría haber puesto eso en un sistema que sí tuviera solución.
Todo tiene solución en esta vida, y la solución a esta pregunta es suspenderte por zopenca...
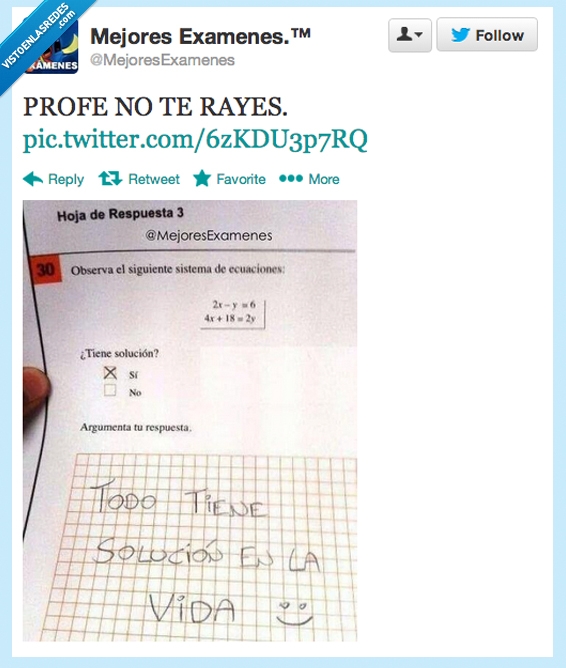
ese sistema de ecuaciones no tiene solución ya que se trata de dos rectas con la misma pendiente, por lo tanto paralelas, con lo que no se cortarán nunca y el sistema no tendrá ninguna solución.
#5 #5 xxxximanolxxxx dijo: ese sistema de ecuaciones no tiene solución ya que se trata de dos rectas con la misma pendiente, por lo tanto paralelas, con lo que no se cortarán nunca y el sistema no tendrá ninguna solución.no se me había ocurrido verlo así
Numéricamente, con unos simples pasos te da 6=9 y por lo tanto sin solucion
#6 #6 kramex dijo: #5 no se me había ocurrido verlo así
Numéricamente, con unos simples pasos te da 6=9 y por lo tanto sin solucionCasi, 6=-9
Habria quedado mejor si hubiera citado a Shakespeare "Los problemas no son eternos, siempre tienen solución, lo único que no se resuelve es la muerte."
Aunque en este caso no, jaja
#5 #5 xxxximanolxxxx dijo: ese sistema de ecuaciones no tiene solución ya que se trata de dos rectas con la misma pendiente, por lo tanto paralelas, con lo que no se cortarán nunca y el sistema no tendrá ninguna solución.En realidad te falta un detalle, podrían tene la misma pendiente pero ser coincidentes, por lo que para que no haya solución también deben ser diferentes los términos independientes de cada ecuación. Cosa que sí sucede.
#9 #9 poetman dijo: #5 En realidad te falta un detalle, podrían tene la misma pendiente pero ser coincidentes, por lo que para que no haya solución también deben ser diferentes los términos independientes de cada ecuación. Cosa que sí sucede.son distintos, basta fijarse...
#6 #6 kramex dijo: #5 no se me había ocurrido verlo así
Numéricamente, con unos simples pasos te da 6=9 y por lo tanto sin solucionla cuestion es que la pregunta dice "observa" no "resuelve", para darse cuenta de que son rectas paralelas no hay que calcular nada. Además el calculo que has hecho está mal.
#5 #5 xxxximanolxxxx dijo: ese sistema de ecuaciones no tiene solución ya que se trata de dos rectas con la misma pendiente, por lo tanto paralelas, con lo que no se cortarán nunca y el sistema no tendrá ninguna solución.A todos los que habéis votado mi comentario como negativo, no os preocupéis, cuando lleguéis a 2º de la ESO os lo explicarán en clase.
En realidad no tiene solucion por que al depejar la y en la de arriba para sustituir en la de abajo las x se anulan por que que +4x a los dos lados y al pasar una al otro lado queda 4x-4x
Vaya nivelazo de matemáticas veo por aquí, vamos... xD
Es un ejercicio de la ESO, joder, ¿os lo tenéis que pensar?
Por cierto, se puede hallar solución al sistema si trabajamos con geometría elíptica.
#7 #7 konas dijo: #6 Casi, 6=-9 sí, perdón, 6=-9
#11 #11 xxxximanolxxxx dijo: #6 la cuestion es que la pregunta dice "observa" no "resuelve", para darse cuenta de que son rectas paralelas no hay que calcular nada. Además el calculo que has hecho está mal.es que es una resolución a ojo. pasas x e y al mismo lado, divides entre dos y lo tienes
#1 #1 Mr_MojoRisin dijo: Si no sabes resolver un sistema de ecuaciones tan fácil como ese... tienes un gran problema.Esa es una prueba que se hace en mi país , Chile. Se llama "Simce" y es dada a alumnos de 4to , 8vo y 2do medio (lo que vendría siendo alumnos de 9 , 13 y 15 años) De ahí que pongan esas respuestas. Pero vamos, que esa prueba nadie se la toma en serio y por eso ponen chorradas
#10 #10 xxxximanolxxxx dijo: #9 son distintos, basta fijarse..."se trata de dos rectas con la misma pendiente y por lo tanto paralelas". Tu has dicho que como tienen la misma pendiente son paralelas, y eso no es cierto. También debe cumplirse la otra condición que te he comentado. No he dicho que en este caso concreto no lo sean.
Deja tu comentario
Necesitas tener una cuenta en VistoenlasRedes.com para poder dejar comentarios.¡Registra tu cuenta ahora!









2 feb 2014, 21:35
Si no sabes resolver un sistema de ecuaciones tan fácil como ese... tienes un gran problema.