Mari, tengo algo que contarte por @Mortimer_Fu
Vía: https://twitter.com/Mortimer_Fu/status/587326012234588160
#1 #1 flowplayer dijo: - Arturo.
- Dime.
- No se dice grados Kelvin sino Kelvin solamente.@flowplayer -Arturo.
-Dime.
-No se pude bajar de los 0 Kelvin.
No tener ni puta idea de si lo que dice tiene algún sentido realmente y darte cuenta de que no por el -1K.
Ese momento cuando no sabes si eres retrasado por no pillarlo o los retrasados son los que lo han aceptado y los comentarios no tienen puto sentido
#4 #4 elrusito dijo: Ese momento cuando no sabes si eres retrasado por no pillarlo o los retrasados son los que lo han aceptado y los comentarios no tienen puto sentido@elrusito +100 para ti, yo estoy igual
#2 #2 hurt_54 dijo: #1 @flowplayer -Arturo.
-Dime.
-No se pude bajar de los 0 Kelvin.@hurt_54 jajajajaja bienvenido al mundo de la termodinámica estadística amigo mío.
No se puede bajar por debajo de 0ºK pero sí que existen temperaturas negativas en la escala Kelvin. Lo sorprendente es que las temperaturas negativas se consiguen CALENTANDO EL SISTEMA. Sí, sí. Calentando el sistema y, por tanto, AUMENTANDO LA TEMPERATURA, hasta que este llega a un máximo de entropía y entonces al meterle más energía la entropía empieza a descender otra vez. La temperatura es una "medida" de como cambia la entropía al dar energía al sistema. Si disminuye al dar energía, la temperatura es negativa.
#6 #6 rotacionaldee dijo: #2 @hurt_54 jajajajaja bienvenido al mundo de la termodinámica estadística amigo mío.
No se puede bajar por debajo de 0ºK pero sí que existen temperaturas negativas en la escala Kelvin. Lo sorprendente es que las temperaturas negativas se consiguen CALENTANDO EL SISTEMA. Sí, sí. Calentando el sistema y, por tanto, AUMENTANDO LA TEMPERATURA, hasta que este llega a un máximo de entropía y entonces al meterle más energía la entropía empieza a descender otra vez. La temperatura es una "medida" de como cambia la entropía al dar energía al sistema. Si disminuye al dar energía, la temperatura es negativa.@rotacionaldee Cuentame más.
No, en serio, me interesa xD Hasta donde yo se, no hay un máximo de entropía, no? Y a t a temperaturas próximas a 0 K, la materia forma un condensado de Bose-Einstein en el que la materia no llega a colapsar por el principio de exclusión, y se elimina toda entropia (a costa de aumentar la entropía del entorno). Como es posible disminuir la entropía a menos de nada?
#7 #7 talking_fox dijo: #6 @rotacionaldee Cuentame más.
No, en serio, me interesa xD Hasta donde yo se, no hay un máximo de entropía, no? Y a t a temperaturas próximas a 0 K, la materia forma un condensado de Bose-Einstein en el que la materia no llega a colapsar por el principio de exclusión, y se elimina toda entropia (a costa de aumentar la entropía del entorno). Como es posible disminuir la entropía a menos de nada?
@talking_fox No soy experto en esto, pero tengo entendido que hay sistemas que sólo pueden acumular una cantidad finita de energía y es en estos sistemas en los que se dan estos casos.
Sí que se puede dar un máximo de entropía. De hecho, es una de las hipótesis que se barajan sobre el fin del universo: https://www.youtube.com/watch?v=4_aOIA-vyBo
Un saludo.
#7 #7 talking_fox dijo: #6 @rotacionaldee Cuentame más.
No, en serio, me interesa xD Hasta donde yo se, no hay un máximo de entropía, no? Y a t a temperaturas próximas a 0 K, la materia forma un condensado de Bose-Einstein en el que la materia no llega a colapsar por el principio de exclusión, y se elimina toda entropia (a costa de aumentar la entropía del entorno). Como es posible disminuir la entropía a menos de nada?
@talking_fox Por cierto, con tu comentario he visto que en mi anterior comentario posiblemente no me expliqué bien. Evidentemente la entropía mínima se da a 0ºK y es S=0 (tercer principio de la termodinámica).
Lo que pasa en estos sistemas es que si les vas metiendo energía la entropía va aumentando hasta su máximo, momento en el que la temperatura vale infinito. En ese momento, si aportas un diferencial de energía más, la entropía empieza a disminuir y la temperatura cambia su valor hasta -infinito, y va creciendo hasta llegar a -0K... sigo en el siguiente comentario...
#7 #7 talking_fox dijo: #6 @rotacionaldee Cuentame más.
No, en serio, me interesa xD Hasta donde yo se, no hay un máximo de entropía, no? Y a t a temperaturas próximas a 0 K, la materia forma un condensado de Bose-Einstein en el que la materia no llega a colapsar por el principio de exclusión, y se elimina toda entropia (a costa de aumentar la entropía del entorno). Como es posible disminuir la entropía a menos de nada?
@talking_fox Sí, es una f*llada mental. Significa que un cuerpo a -10ºK cede calor a un cuerpo a 100ºK, por ejemplo. Si quieres saber más pregunta a algún físico, ya que yo estudio ingeniería y hasta aquí llegan mis conocimientos sobre este tema.
Un saludo de nuevo.
#1 #1 flowplayer dijo: - Arturo.
- Dime.
- No se dice grados Kelvin sino Kelvin solamente.@flowplayer Emm, no se que te han enseñado a ti pero si que se dice grados kelvin, pues es una escala de temperatura.
#6 #6 rotacionaldee dijo: #2 @hurt_54 jajajajaja bienvenido al mundo de la termodinámica estadística amigo mío.
No se puede bajar por debajo de 0ºK pero sí que existen temperaturas negativas en la escala Kelvin. Lo sorprendente es que las temperaturas negativas se consiguen CALENTANDO EL SISTEMA. Sí, sí. Calentando el sistema y, por tanto, AUMENTANDO LA TEMPERATURA, hasta que este llega a un máximo de entropía y entonces al meterle más energía la entropía empieza a descender otra vez. La temperatura es una "medida" de como cambia la entropía al dar energía al sistema. Si disminuye al dar energía, la temperatura es negativa.@rotacionaldee Tío aquí se escribe en castellano, no sé dónde te habrás comprado ese teclado chino pero mejor lo tiras a la basura
#1 #1 flowplayer dijo: - Arturo.
- Dime.
- No se dice grados Kelvin sino Kelvin solamente.@flowplayer #12 #12 shurmanico dijo: #6 @rotacionaldee Tío aquí se escribe en castellano, no sé dónde te habrás comprado ese teclado chino pero mejor lo tiras a la basura@shurmanico Si lo lamentable del tema es "la incultura al poder"... aunque ya sé, lo dirás con ironía. De todos modos, para mencionar el condensado Böse-Einstein, éste no es el sitio, desde luego.
#8 #8 rotacionaldee dijo: #7 @talking_fox No soy experto en esto, pero tengo entendido que hay sistemas que sólo pueden acumular una cantidad finita de energía y es en estos sistemas en los que se dan estos casos.
Sí que se puede dar un máximo de entropía. De hecho, es una de las hipótesis que se barajan sobre el fin del universo: https://www.youtube.com/watch?v=4_aOIA-vyBo
Un saludo.@rotacionaldee8 Pues aun con todo lo que he leído acerca de física del universo, nunca se me había ocurrido plantearme que pasaría con la entropía en un posible "Big Crunch", parece mentira...
Muy interesante el vídeo, y gracias por tu explicación ;)
Un saludo.
#13 #13 shouseillo dijo: #1 @flowplayer #12 @shurmanico Si lo lamentable del tema es "la incultura al poder"... aunque ya sé, lo dirás con ironía. De todos modos, para mencionar el condensado Böse-Einstein, éste no es el sitio, desde luego.@shouseillo Vale, perdón, la próxima vez preguntaré mi duda vía paloma mensajera xD
Deja tu comentario
Necesitas tener una cuenta en VistoenlasRedes.com para poder dejar comentarios.¡Registra tu cuenta ahora!
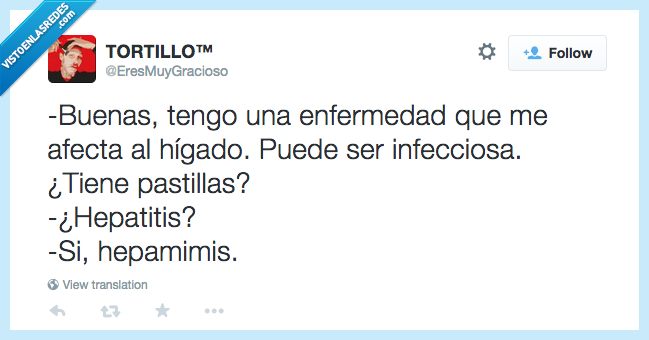
¿Está usted enfermo? por @EresMuyGracioso
Vía: https://twitter.com/EresMuyGracioso/status/589001223279370240
¡Campaaaaaana y se acabó! por @Gafasaos
Vía: https://twitter.com/Gafasaos/status/588788032028958720
Lo nunca visto, no tiene emoción por @Profeta_Baruc
Vía: https://twitter.com/Profeta_Baruc/status/587363559165812736











18 abr 2015, 18:49
- Arturo.
- Dime.
- No se dice grados Kelvin sino Kelvin solamente.