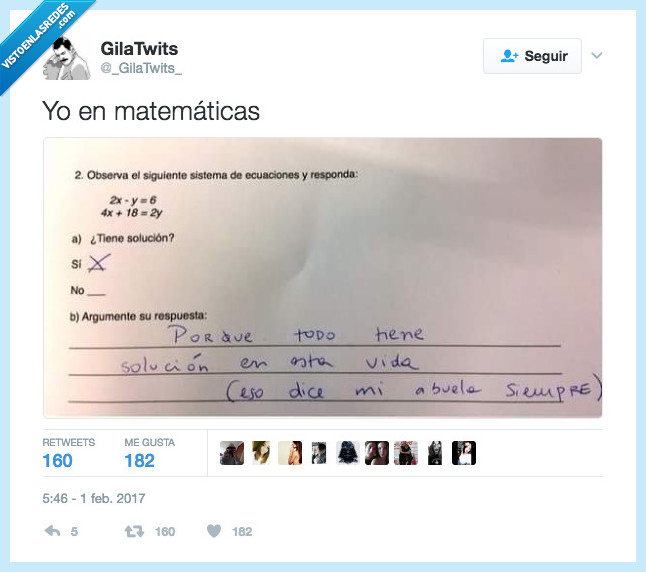
Cuando no se te dan bien las matemáticas pero eres positivo por @_GilaTwits_
Vía: https://twitter.com/_GilaTwits_/status/826819110394802176
#1 #1 geheimnis dijo: Pues eso en concreto no la tiene. Mala suerte.@geheimnis En realidad si tiene solución. Es un sistema compatible indeterminado y como tal tiene infinitas soluciones. Concretamente este: y=lambda , x=(6+lambda)/2.
#2 #2 wason12 dijo: #1 @geheimnis En realidad si tiene solución. Es un sistema compatible indeterminado y como tal tiene infinitas soluciones. Concretamente este: y=lambda , x=(6+lambda)/2.@wason12 si reduces la segunda ecuación queda 2x - y = - 9 mientras que la primera es 2x - y = 6. No tiene solución.
La matriz de coeficientes tiene como columnas los vectores {(2, 4),(-1,-2)} que, obviamente no constituye una base de R2, pero sí de R1. Sin embargo la matriz ampliada tiene como columnas los vectores {(2, 4),(-1,-2), (6, -18)}, que es equivalente al generado por la base de R2: {(1,2),(1,-2)}. Puesto que la matriz de coeficientes y la ampliada corresponden a bases de diferente dimensión por el teorema de Rouché el sistema de ecuaciones es incompatible.
(Como veo que os poneis divinos con las matematicas, me uno al circo de pedantes)
#3 #3 geheimnis dijo: #2 @wason12 si reduces la segunda ecuación queda 2x - y = - 9 mientras que la primera es 2x - y = 6. No tiene solución.@geheimnis Pues he quedado fatal. Me lo merezco por ir de pedante XD
#2 #2 wason12 dijo: #1 @geheimnis En realidad si tiene solución. Es un sistema compatible indeterminado y como tal tiene infinitas soluciones. Concretamente este: y=lambda , x=(6+lambda)/2.@wason12 no tiene si lo haces por reduccion te queda 0 = 24 por lo que es un sistema indeterminado para que sea compatible indeterminado te tiene que dar 0=0
Deja tu comentario
Necesitas tener una cuenta en VistoenlasRedes.com para poder dejar comentarios.¡Registra tu cuenta ahora!
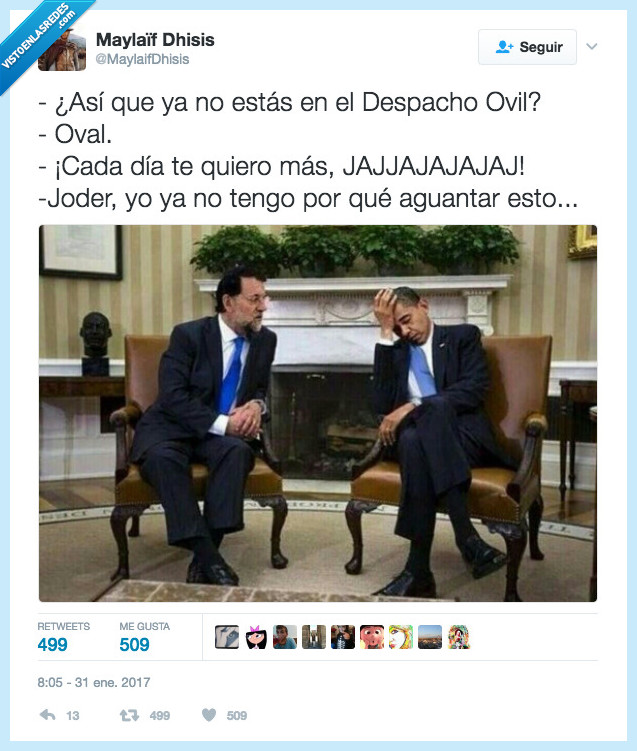
¿De verdad eres tan tonto o te lo haces? por @MaylaifDhisis
Vía: https://twitter.com/MaylaifDhisis/status/826491555066281984
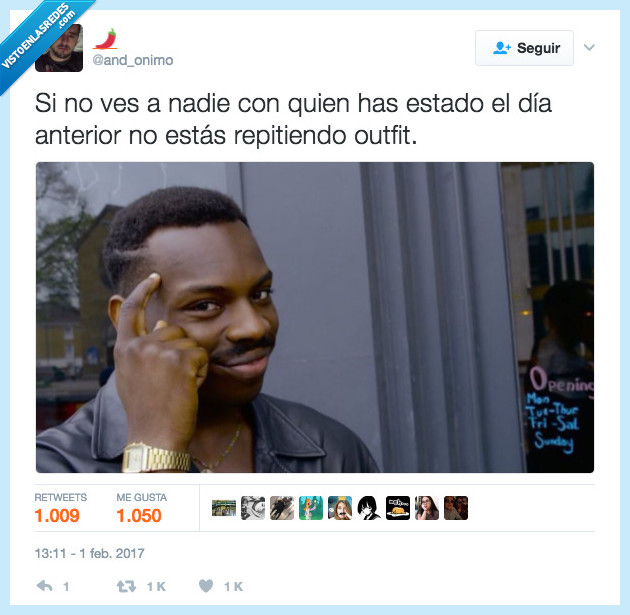
Lo malo es que te pases así 3 días que empiezas a echar peste por @and_onimo
Vía: https://twitter.com/and_onimo/status/826931083241517056









3 feb 2017, 14:36
Pues eso en concreto no la tiene. Mala suerte.